リアクタンスとコイルの誘導性リアクタンスが同じになり
ます。直列回路ではあの黄金公式に入れたらリアクタンス
は消滅してこの場合ですと抵抗だけになる、つまり直列
回路では電流が最大になります、これが直列共振状態です。
次にLとCの並列回路でその合成インピーダンスZを求めて
式を変形、最後にXL=XCとするとZは無限大∞になります。
流れる電流は当然最小値です、この状態を並列共振状態
というのです。共振回路のコアとはこういう意味です。
共振周波数fはωL=1/ωC⇒2πfL=1(2πfc)から求める！
ここを理解してれば文章問題や基本的なA問題の共振
問題は大丈夫です。
本でよく見る説明ですがコイルとコンデンサーに流れる
電流が同じならIRだけとなります。位相が逆なので接続
点から電源側のそれらの影響は消える、ただ素子に流れ
る各電流は変わりません。接続点から見た場合にLC並列
部分の抵抗が∞にになったわけです。この形の出題があ
ったら共振状態ではないか？を必ず疑いましょう。
電験三種理論を受験するなら必須とも言える共振回路、過去
10年分から本当に理解してないと解けない計算問題４選。
まずこの問題はインダクタンスと静電容量の加算を知ってれ
ばこの様に共振周波数の公式に代入して最後は機械的に比較
すればいんです。
最後分数では微量な大きさの違いがピンときません！
下の問題は電源周波数が10Hzと10MHzになった時の主電流
の変化率を求めるのです。
10Hzの時にリアクタンスが等しいという事は並列共振
つまりCとLがないのと同じなのでR1+R2で流れる電流を
求めます。
コンデンサーリアクタンスは大きいためほとんど電流
が流れない、逆にコイルリアクタンスは小さいため
ほぼ導通状態と考えると抵抗R1のみで流れる電流と
考えます。こういう考え方で計算するのは珍しいの
で覚えておきましょう、他例の計算でも使えます。
下の問題は回路インピーダンスを複素数計算しない事
には何も検証できません。
インピーダンスを最大にするためには
ここで変化するのは周波数、つまりωだから虚数部が
最大になればいい、そうなると下のあの部分を=0にす
ればいいのです、そこから式を変形してω２を求める
インピーダンスを最小にするためには
虚数部=0になればいいのですから下の関係を考えます。
10の乗数を平方根から最後出すためには10の５乗とか
奇数では関数電卓が試験では使えない、だから0.1を
掛けてあそこを10のー２乗にしました。最終的にω1
を求める事ができます。
下の問題、電源電圧が1Vしかないのでかなり扱う値が小さく
なるため近似とかせずにJUSTで求める必要があると判断して
こういう計算処理をしました。ω単位はKの1000です、又
5Kradは5ではなく5000で扱います。
途中でCとLの値を入れて検証のための式を完成させます。
これに３パターンのωを入れて検証できます
してる計算は難解ではないけど、正直メンドウと思いました。
ただ正確には計算できました。10Kradの時に並列共振するのが
わかります。
最後これらの問題は貴方が解いてみてください。
これで電験三種共振回路については完璧ですね。
A問題として出題なら通常はこのレベルです。
★共振回路の問題は2021年に1問は出る可能性あり
問題の丸暗記ではなくて共振回路の中身を理解
この２問が解けないでは試験を受けてもまだヤバイです。
★⇒電験三種基礎最新記事へ
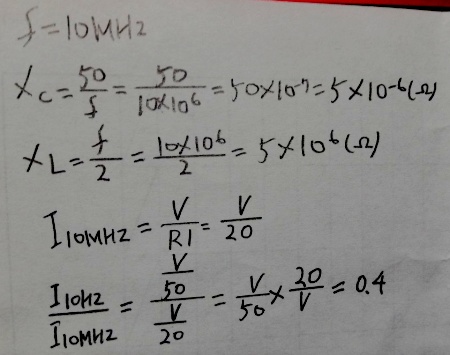
0 件のコメント:
コメントを投稿